The modeling and simulation of genetic regulatory networks are currently subject to two major constraints. In the first place, the biochemical reaction mechanisms underlying regulatory interactions are usually not or incompletely known. In the second place, quantitative information on kinetic parameters and molecular concentrations is only seldom available, even in the case of well-studied model systems. As a consequence, traditional, numerical methods for modeling and simulation are often difficult to apply.
The method for the qualitative modeling and simulation of genetic regulatory networks developed in the HELIX group is able to handle the above two constraints. Following ideas originally proposed by Glass and Kaufmann, the networks are modeled by a class of piecewise-linear (PL) differential equations. The state variables in the models correspond to the concentrations of proteins encoded by the genes in the network, while the differential equations represent the interactions through which certain proteins influence the synthesis and degradation of other proteins. The regulatory interactions are modeled by step functions, justified by the observation that the activation of a gene, as a function of the concentration of regulatory protein, often follows a steep sigmoid function.
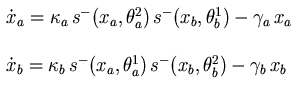
Genetic regulatory network and piecewise-linear differential equations describing the network. |
Instead of giving numerical values to the parameters, the qualitative simulation method supplements the PL differential equations by inequality constraints on the parameters. These inequality constraints have a clear biological meaning and can be inferred from the biological literature. On the one hand, the inequality constraints divide the phase space into regions corresponding to qualitative states of the system. On the other hand, they allow the possible transitions between qualitative states to be determined by exploiting the simple mathematical form of the PL models. A qualitative simulation consists of the generation of all qualitative states that are reachable through one or more transitions from a given initial state. The simulation results have the form of a state transition graph composed of qualitative states and transitions between qualitative states. The paths in this graph represent the possible qualitative behaviors of the system.
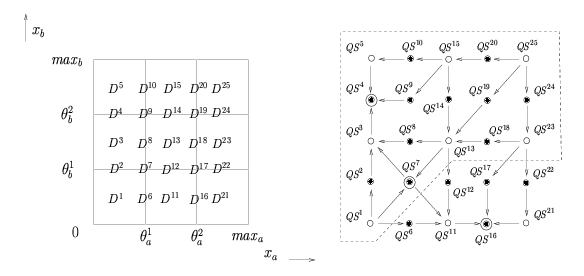 Subdivision of the phase space into regions and the corresponding state transition graph describing the qualitative dynamics of the genetic regulatory network. Subdivision of the phase space into regions and the corresponding state transition graph describing the qualitative dynamics of the genetic regulatory network. |
Literature
H. de Jong, J.-L. Gouzé, C. Hernandez, M. Page, T. Sari, J. Geiselmann (2003), Hybrid modeling and simulation of genetic regulatory networks: A qualitative approach, A. Pnueli, O. Maler (eds), Hybrid Systems: Computation and Control (HSCC 2003), Lecture Notes in Computer Science 2623, Springer-Verlag, Berlin, 267-282.
H. de Jong, J.-L. Gouzé, C. Hernandez, M. Page, T. Sari, J. Geiselmann (2004), Qualitative simulation of genetic regulatory networks using piecewise-linear models, Bulletin of Mathematical Biology, 66(2):301-340.
L. Glass, S.A. Kauffman (1973), The logical analysis of continuous non-linear biochemical control networks, Journal of Theoretical Biology, 39(1):103-129.
R. Thomas, R. d'Ari (1990), Biological Feedback, CRC Press, Boca Raton, FL. |